5th Postulate Of Euclidean Geometry

Geometric axiom

If the sum of the interior angles α and β is less than 180°, the ii directly lines, produced indefinitely, meet on that side.

In geometry, the parallel postulate, also called Euclid'south 5th postulate because it is the fifth postulate in Euclid's Elements, is a distinctive axiom in Euclidean geometry. Information technology states that, in ii-dimensional geometry:

If a line segment intersects two direct lines forming two interior angles on the same side that are less than ii right angles, then the two lines, if extended indefinitely, meet on that side on which the angles sum to less than two right angles.

This postulate does not specifically talk almost parallel lines;^[1] information technology is only a postulate related to parallelism. Euclid gave the definition of parallel lines in Book I, Definition 23^[2] just before the v postulates.^[3]

Euclidean geometry is the study of geometry that satisfies all of Euclid's axioms, including the parallel postulate.

The postulate was long considered to be obvious or inevitable, but proofs were elusive. Somewhen, it was discovered that inverting the postulate gave valid, albeit different geometries. A geometry where the parallel postulate does non hold is known as a non-Euclidean geometry. Geometry that is independent of Euclid'due south fifth postulate (i.eastward., only assumes the modern equivalent of the first four postulates) is known as absolute geometry (or sometimes "neutral geometry").

Equivalent properties [edit]

Probably the best-known equivalent of Euclid'southward parallel postulate, contingent on his other postulates, is Playfair's axiom, named after the Scottish mathematician John Playfair, which states:

In a plane, given a line and a point not on it, at most 1 line parallel to the given line can exist drawn through the point. ^[iv]

This precept by itself is non logically equivalent to the Euclidean parallel postulate since there are geometries in which 1 is truthful and the other is non. Still, in the presence of the remaining axioms which requite Euclidean geometry, each of these can be used to evidence the other, and then they are equivalent in the context of absolute geometry.^[5]

Many other statements equivalent to the parallel postulate have been suggested, some of them appearing at first to be unrelated to parallelism, and some seeming and so cocky-evident that they were unconsciously causeless by people who claimed to accept proven the parallel postulate from Euclid's other postulates. These equivalent statements include:

In that location is at most 1 line that can be drawn parallel to another given one through an external point. (Playfair's axiom)
The sum of the angles in every triangle is 180° (triangle postulate).
There exists a triangle whose angles add up to 180°.
The sum of the angles is the same for every triangle.
There exists a pair of similar, but not congruent, triangles.
Every triangle can be circumscribed.
If three angles of a quadrilateral are right angles, and then the quaternary bending is also a right angle.
There exists a quadrilateral in which all angles are right angles, that is, a rectangle.
There exists a pair of straight lines that are at constant distance from each other.
Ii lines that are parallel to the same line are also parallel to each other.
In a correct-angled triangle, the foursquare of the hypotenuse equals the sum of the squares of the other ii sides (Pythagoras' theorem).^[6] ^[vii]
The law of cosines, a generalization of Pythagoras' theorem.
There is no upper limit to the area of a triangle. (Wallis precept)^[8]
The summit angles of the Saccheri quadrilateral are 90°.
If a line intersects i of 2 parallel lines, both of which are coplanar with the original line, so it also intersects the other. (Proclus' axiom)^[9]

Notwithstanding, the alternatives which employ the word "parallel" cease appearing and so unproblematic when 1 is obliged to explain which of the four common definitions of "parallel" is meant – abiding separation, never meeting, same angles where crossed by some third line, or same angles where crossed past any tertiary line – since the equivalence of these four is itself 1 of the unconsciously obvious assumptions equivalent to Euclid's fifth postulate. In the list in a higher place, it is always taken to refer to not-intersecting lines. For example, if the word "parallel" in Playfair's precept is taken to mean 'constant separation' or 'same angles where crossed by any third line', then it is no longer equivalent to Euclid'south 5th postulate, and is provable from the first four (the axiom says 'There is at most one line...', which is consistent with there beingness no such lines). However, if the definition is taken so that parallel lines are lines that do non intersect, or that have some line intersecting them in the same angles, Playfair's axiom is contextually equivalent to Euclid's fifth postulate and is thus logically independent of the first four postulates. Note that the latter two definitions are not equivalent, because in hyperbolic geometry the 2nd definition holds but for ultraparallel lines.

History [edit]

From the beginning, the postulate came under attack every bit being provable, and therefore non a postulate, and for more than 2 thousand years, many attempts were made to prove (derive) the parallel postulate using Euclid's first 4 postulates.^[10] The main reason that such a proof was then highly sought subsequently was that, different the first iv postulates, the parallel postulate is not self-evident. If the order in which the postulates were listed in the Elements is meaning, it indicates that Euclid included this postulate just when he realised he could not testify it or proceed without it.^[11] Many attempts were made to bear witness the 5th postulate from the other iv, many of them being accustomed equally proofs for long periods until the mistake was found. Invariably the fault was assuming some 'obvious' belongings which turned out to exist equivalent to the fifth postulate (Playfair'due south axiom). Although known from the time of Proclus, this became known as Playfair's Precept subsequently John Playfair wrote a famous commentary on Euclid in 1795 in which he proposed replacing Euclid's fifth postulate past his own axiom. Today, over two m two hundred years later, Euclid'due south fifth postulate remains a postulate.

Proclus (410–485) wrote a commentary on The Elements where he comments on attempted proofs to deduce the 5th postulate from the other four; in particular, he notes that Ptolemy had produced a simulated 'proof'. Proclus and then goes on to give a false proof of his ain. However, he did give a postulate which is equivalent to the 5th postulate.

Ibn al-Haytham (Alhazen) (965-1039), an Arab mathematician, fabricated an effort at proving the parallel postulate using a proof by contradiction,^[12] in the course of which he introduced the concept of motion and transformation into geometry.^[13] He formulated the Lambert quadrilateral, which Boris Abramovich Rozenfeld names the "Ibn al-Haytham–Lambert quadrilateral",^[14] and his attempted proof contains elements like to those plant in Lambert quadrilaterals and Playfair's precept.^[15]

The Persian mathematician, astronomer, philosopher, and poet Omar Khayyám (1050–1123), attempted to prove the fifth postulate from another explicitly given postulate (based on the 4th of the 5 principles due to the Philosopher (Aristotle), namely, "Ii convergent straight lines intersect and it is impossible for two convergent straight lines to diverge in the direction in which they converge."^[16] He derived some of the before results belonging to elliptical geometry and hyperbolic geometry, though his postulate excluded the latter possibility.^[17] The Saccheri quadrilateral was likewise starting time considered by Omar Khayyám in the late 11th century in Volume I of Explanations of the Difficulties in the Postulates of Euclid.^[xiv] Different many commentators on Euclid before and after him (including Giovanni Girolamo Saccheri), Khayyám was not trying to prove the parallel postulate equally such just to derive it from his equivalent postulate. He recognized that iii possibilities arose from omitting Euclid's fifth postulate; if two perpendiculars to one line cross another line, judicious choice of the last can make the internal angles where information technology meets the two perpendiculars equal (information technology is then parallel to the first line). If those equal internal angles are right angles, we get Euclid's fifth postulate, otherwise, they must be either acute or birdbrained. He showed that the acute and birdbrained cases led to contradictions using his postulate, but his postulate is now known to be equivalent to the 5th postulate.

Nasir al-Din al-Tusi (1201–1274), in his Al-risala al-shafiya'an al-shakk fi'50-khutut al-mutawaziya (Discussion Which Removes Dubiousness nearly Parallel Lines) (1250), wrote detailed critiques of the parallel postulate and on Khayyám's attempted proof a century earlier. Nasir al-Din attempted to derive a proof by contradiction of the parallel postulate.^[18] He also considered the cases of what are now known as elliptical and hyperbolic geometry, though he ruled out both of them.^[17]

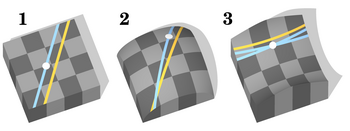
Euclidean, elliptical and hyperbolic geometry. The Parallel Postulate is satisfied just for models of Euclidean geometry.

Nasir al-Din's son, Sadr al-Din (sometimes known as "Pseudo-Tusi"), wrote a book on the subject in 1298, based on his father's later thoughts, which presented one of the earliest arguments for a non-Euclidean hypothesis equivalent to the parallel postulate. "He essentially revised both the Euclidean system of axioms and postulates and the proofs of many propositions from the Elements."^[18] ^[xix] His work was published in Rome in 1594 and was studied by European geometers. This work marked the starting point for Saccheri'southward work on the subject^[18] which opened with a criticism of Sadr al-Din'due south work and the piece of work of Wallis.^[20]

Giordano Vitale (1633-1711), in his book Euclide restituo (1680, 1686), used the Khayyam-Saccheri quadrilateral to prove that if three points are equidistant on the base AB and the top CD, then AB and CD are everywhere equidistant. Girolamo Saccheri (1667-1733) pursued the same line of reasoning more thoroughly, correctly obtaining absurdity from the obtuse case (proceeding, like Euclid, from the implicit assumption that lines tin can be extended indefinitely and have infinite length), but declining to abnegate the acute case (although he managed to wrongly persuade himself that he had).

In 1766 Johann Lambert wrote, but did not publish, Theorie der Parallellinien in which he attempted, equally Saccheri did, to prove the fifth postulate. He worked with a effigy that today we call a Lambert quadrilateral, a quadrilateral with three right angles (tin can exist considered half of a Saccheri quadrilateral). He quickly eliminated the possibility that the fourth angle is obtuse, as had Saccheri and Khayyám, and then proceeded to prove many theorems under the assumption of an acute angle. Unlike Saccheri, he never felt that he had reached a contradiction with this assumption. He had proved the non-Euclidean upshot that the sum of the angles in a triangle increases every bit the expanse of the triangle decreases, and this led him to speculate on the possibility of a model of the astute case on a sphere of imaginary radius. He did not carry this thought any further.^[21]

Where Khayyám and Saccheri had attempted to evidence Euclid's fifth by disproving the simply possible alternatives, the nineteenth century finally saw mathematicians exploring those alternatives and discovering the logically consistent geometries that outcome. In 1829, Nikolai Ivanovich Lobachevsky published an business relationship of astute geometry in an obscure Russian journal (afterward re-published in 1840 in German). In 1831, János Bolyai included, in a volume by his begetter, an appendix describing astute geometry, which, doubtlessly, he had developed independently of Lobachevsky. Carl Friedrich Gauss had also studied the problem, but he did not publish any of his results. Upon hearing of Bolyai'southward results in a letter of the alphabet from Bolyai'south begetter, Farkas Bolyai, Gauss stated:

"If I commenced past saying that I am unable to praise this piece of work, you would certainly be surprised for a moment. But I cannot say otherwise. To praise it would be to praise myself. Indeed the whole contents of the work, the path taken by your son, the results to which he is led, coincide well-nigh entirely with my meditations, which take occupied my mind partly for the last thirty or xxx-five years."^[22]

The resulting geometries were later developed by Lobachevsky, Riemann and Poincaré into hyperbolic geometry (the acute case) and elliptic geometry (the birdbrained case). The independence of the parallel postulate from Euclid's other axioms was finally demonstrated by Eugenio Beltrami in 1868.

Converse of Euclid'south parallel postulate [edit]

The converse of the parallel postulate: If the sum of the two interior angles equals 180°, then the lines are parallel and will never intersect.

Euclid did not postulate the converse of his 5th postulate, which is one way to distinguish Euclidean geometry from elliptic geometry. The Elements contains the proof of an equivalent statement (Book I, Suggestion 27): If a directly line falling on two straight lines make the alternate angles equal to 1 another, the straight lines will be parallel to one another. As De Morgan^[23] pointed out, this is logically equivalent to (Book I, Proposition xvi). These results do not depend upon the fifth postulate, merely they do require the second postulate^[24] which is violated in elliptic geometry.

Criticism [edit]

Attempts to logically prove the parallel postulate, rather than the 8th axiom,^[25] were criticized past Arthur Schopenhauer in The World as Volition and Idea. Still, the argument used past Schopenhauer was that the postulate is evident past perception, not that it was not a logical consequence of the other axioms.^[26]

Decomposition of the parallel postulate [edit]

The parallel postulate is equivalent, as shown in,^[27] to the conjunction of the Lotschnittaxiom and of Aristotle's precept. The former states that the perpendiculars to the sides of a right angle intersect, while the latter states that in that location is no upper bound for the lengths of the distances from the leg of an bending to the other leg. As shown in,^[28] the parallel postulate is equivalent to the conjunction of the following incidence-geometric forms of the Lotschnittaxiom and of Aristotle's precept:

Given three parallel lines, at that place is a line that intersects all three of them.

Given a line a and two singled-out intersecting lines m and due north, each unlike from a, at that place exists a line k which intersects a and thou, but not n.

Every bit shown in,^[29] the splitting of the parallel postulate into the conjunction of these incidence-geometric axioms is possible only in the presence of absolute geometry.

Notes [edit]

^ not-Euclidean geometries, by Dr. Katrina Piatek-Jimenez
^ "Euclid's Elements, Book I, Definition 23". Clark University . Retrieved 2022-04-19 . Parallel straight lines are directly lines which, being in the same aeroplane and existence produced indefinitely in both directions, do not run across 1 another in either direction.
^ Euclid'south Elements, Volume I
^ Euclid's Parallel Postulate and Playfair's Axiom
^ Henderson & Taimiņa 2005, pg. 139
^ Eric W. Weisstein (2003), CRC concise encyclopedia of mathematics (second ed.), p. 2147, ISBNi-58488-347-2, The parallel postulate is equivalent to the Equidistance postulate, Playfair axiom, Proclus axiom, the Triangle postulate and the Pythagorean theorem.
^ Alexander R. Pruss (2006), The principle of sufficient reason: a reassessment, Cambridge University Press, p. 11, ISBN0-521-85959-10, We could include...the parallel postulate and derive the Pythagorean theorem. Or we could instead make the Pythagorean theorem amid the other axioms and derive the parallel postulate.
^ Bogomolny, Alexander. "Euclid's Fifth Postulate". Cut The Knot . Retrieved 30 September 2011.
^ Weisstein, Eric W. "Proclus' Precept – MathWorld". Retrieved 2009-09-05 .
^ Euclid; Heath, Thomas Piffling, Sir (1956). The thirteen books of Euclid's Elements. New York: Dover Publications. p. 202. ISBN0-486-60088-2. OCLC 355237.
^ Florence P. Lewis (January 1920), "History of the Parallel Postulate", The American Mathematical Monthly, The American Mathematical Monthly, Vol. 27, No. i, 27 (1): 16–23, doi:ten.2307/2973238, JSTOR 2973238.
^ Katz 1998, pg. 269
^ Katz 1998, p. 269:

In effect, this method characterized parallel lines every bit lines always equidistant from one another and besides introduced the concept of motion into geometry.
^ ^a ^b Rozenfeld 1988, p. 65
^ Smith 1992
^ Boris A Rosenfeld and Adolf P Youschkevitch (1996), Geometry, p.467 in Roshdi Rashed, Régis Morelon (1996), Encyclopedia of the history of Arabic science, Routledge, ISBN 0-415-12411-5.
^ ^a ^b Boris A. Rosenfeld and Adolf P. Youschkevitch (1996), "Geometry", in Roshdi Rashed, ed., Encyclopedia of the History of Arabic Science, Vol. 2, p. 447-494 [469], Routledge, London and New York:

"Khayyam'south postulate had excluded the case of the hyperbolic geometry whereas al-Tusi's postulate ruled out both the hyperbolic and elliptic geometries."
^ ^a ^b ^c Katz 1998, pg.271:

"But in a manuscript probably written by his son Sadr al-Din in 1298, based on Nasir al-Din's later thoughts on the field of study, there is a new argument based on some other hypothesis, likewise equivalent to Euclid's, [...] The importance of this latter piece of work is that information technology was published in Rome in 1594 and was studied by European geometers. In detail, it became the starting point for the work of Saccheri and ultimately for the discovery of non-Euclidean geometry."
^ Boris A. Rosenfeld and Adolf P. Youschkevitch (1996), "Geometry", in Roshdi Rashed, ed., Encyclopedia of the History of Arabic Science, Vol. two, p. 447-494 [469], Routledge, London and New York:

"In Pseudo-Tusi's Exposition of Euclid, [...] another statement is used instead of a postulate. It was contained of the Euclidean postulate V and easy to prove. [...] He essentially revised both the Euclidean organisation of axioms and postulates and the proofs of many propositions from the Elements."
^ MacTutor's Giovanni Girolamo Saccheri
^ O'Connor, J.J.; Robertson, E.F. "Johann Heinrich Lambert". Retrieved 16 September 2011.
^ Faber 1983, pg. 161
^ Heath, T.L., The thirteen books of Euclid's Elements, Vol.ane, Dover, 1956, pg.309.
^ Coxeter, H.Due south.Thousand., Non-Euclidean Geometry, 6th Ed., MAA 1998, pg.3
^ Schopenhauer is referring to Euclid's Common Notion 4: Figures coinciding with ane another are equal to one another.
^ http://www.gutenberg.org/files/40097/40097-pdf.pdf^{[ blank URL PDF ]}
^ Pambuccian, Victor (1994), "Zum Stufenaufbau des Parallelenaxioms", Journal of Geometry, 51 (1–2): 79–88, doi:10.1007/BF01226859, hdl:2027.42/43033, S2CID 28056805
^ Pambuccian, Victor; Schacht, Celia (2021), "The ubiquitous axiom", Results in Mathematics, 76 (3): one–39, doi:10.1007/s00025-021-01424-3, S2CID 236236967
^ Pambuccian, Victor (2022), "On a splitting of the parallel postulate", Journal of Geometry, 113 (1): 1–13, doi:10.1007/s00022-022-00626-six, S2CID 246281748

References [edit]

Carroll, Lewis, Euclid and His Modern Rivals, Dover, ISBN 0-486-22968-8
Faber, Richard Fifty. (1983), Foundations of Euclidean and Not-Euclidean Geometry, New York: Marcel Dekker Inc., ISBN0-8247-1748-1
Henderson, David Due west.; Taimiņa, Daina (2005), Experiencing Geometry: Euclidean and Non-Euclidean with History (3rd ed.), Upper Saddle River, NJ: Pearson Prentice Hall, ISBN0-thirteen-143748-eight
Katz, Victor J. (1998), History of Mathematics: An Introduction , Addison-Wesley, ISBN0-321-01618-1, OCLC 38199387
Rozenfeld, Boris A. (1988), A History of Non-Euclidean Geometry: Evolution of the Concept of a Geometric Space, Springer Scientific discipline+Business Media, ISBN0-387-96458-4, OCLC 15550634
Smith, John D. (1992), "The Remarkable Ibn al-Haytham", The Mathematical Gazette, Mathematical Association, 76 (475): 189–198, doi:10.2307/3620392, JSTOR 3620392, S2CID 118597450
Boutry, Pierre; Gries, Charly; Narboux, Julien; Schreck, Pascal (2019), "Parallel postulates and continuity axioms: a mechanized study in intuitionistic logic using Coq", Periodical of Automatic Reasoning, 62: one–68, doi:ten.1007/s10817-017-9422-viii, S2CID 25900234
Pambuccian, Victor; Schacht, Celia (2021), "The ubiquitous axiom", Results in Mathematics, 76 (3): 1–39, doi:10.1007/s00025-021-01424-three, S2CID 236236967
Pambuccian, Victor (2022), "On a splitting of the parallel postulate", Journal of Geometry, 113 (1): 1–xiii, doi:10.1007/s00022-022-00626-6, S2CID 246281748

External links [edit]

On Gauss' Mountains

Eder, Michelle (2000), Views of Euclid's Parallel Postulate in Ancient Greece and in Medieval Islam, Rutgers University, retrieved 2008-01-23